
Андреев С. С., Дбар С. А., Лацис А. О., Плоткина Е. А.
Гибридный реконфигурируемый вычислитель.
Руководство программиста.
Часть 2. Типовые приемы программирования.
За счет чего схемная реализация работает быстрее программной?
Примеры схем, приведенные в Части 1 настоящего Руководства, дают некоторое начальное представление о языке Автокод HDL. При этом совершенно не проясненным остается главный вопрос: почему использование именно этого, такого непривычного и сложного, языка дает программисту шанс многократно ускорить выполнение расчета? Какую именно содержательную информацию о свойствах алгоритма, утрачиваемую при записи на С или Фортране, именно этот язык позволяет донести до аппаратуры, заставляя ее работать быстрее? Не поняв этого, хотя бы в общих чертах, надеяться на ускорение схемной реализации расчета, по сравнению с программной, бессмысленно.
Начнем с грубой оценки. Процессор (Pentium, Opteron, …) является цифровой электронной схемой на базе транзисторов, как и та схема сопроцессора, которую мы описываем на Автокоде HDL, загружая результат трансляции этого описания в модуль программируемой логики. Чтобы одна цифровая электронная схема (наш сопроцессор) работала быстрее другой (стандартный процессор общего назначения), она, казалось бы, должна либо содержать больше исходного материала (транзисторов) для построения большего числа арифметических устройств, либо иметь более высокую частоту работы этих устройств. В данном случае ни одно из этих утверждений не верно – по «количеству исходного материала» модуль программируемой логики близок к современному микропроцессору общего назначения, а по тактовой частоте отстает от него примерно на порядок (в 7-20 раз). Тем самым, грубая оценка показывает, что вместо выигрыша схемная реализация, казалось бы, должна давать заметный скоростной проигрыш. Тем не менее, ускорение реальных расчетов при грамотной схемной реализации – экспериментальный факт. Так откуда же все-таки оно берется?
Ситуация только кажется парадоксальной. В действительности, программистам хорошо известна очень похожая ситуация, возникающая при использовании интерпретируемых языков программирования.
Попробуйте записать Ваш расчет на таком языке, как Perl, Python или Java, и сравните быстродействие полученной программы с быстродействием программы, написанной на Фортране или С. Программа на интерпретируемом языке будет работать в разы, а то и в десятки раз медленнее. При этом полезной, с точки зрения программиста, работы она выполняет столько же, и использует тот же самый процессор, что и программа на компилируемом языке. Причина этого, как мы хорошо знаем, в том, что при выполнении программы на интерпретируемом языке процессор занят, в основном, работой «бесполезной». Он лишь изредка выполняет записанные в программе арифметические вычисления, тратя основное время на выяснение того, какие именно вычисления, и с какими данными, надо выполнять в данный момент, то есть на интерпретацию программы.
Компилируя программу, мы выполняем эту «бесполезную» работу заранее, избавляя процессор от нее на фазе выполнения программы. Выполняя скомпилированную программу, процессор работает не быстрее, но с гораздо более высоким к.п.д., что и ускоряет расчет.
Вся ли «бесполезная» работа выполняется заранее при компиляции программы, написанной на традиционном языке программирования? Снова используем грубую оценку. Сравним реально достигаемое при выполнении программы быстродействие в «полезных» арифметических операциях с заявленным производителем процессора пиковым быстродействием. Получаемая величина «к.п.д.» для подавляющего большинства реальных программ вычислительного характера будет лежать в диапазоне от 1 до 15 процентов, чаще всего – в районе 3-5 процентов. Следовательно, даже выполняя заранее скомпилированную программу, процессор тратит практически все время на «бесполезную» работу по подготовке к вычислениям, и лишь малую его часть – на сами вычисления. Для того, чтобы исключить (или многократно снизить) уже эти затраты, программу, похоже, надо «скомпилировать еще раз».
Заменив программу на интерпретируемом языке машинной программой на языке команд процессора, мы многократно сократили работу по интерпретации программы, но ни в коей мере не ликвидировали ее как таковую. Процессор по-прежнему «не знает заранее», что именно ему предстоит делать, и интерпретирует программу, команду за командой, всякий раз выясняя, каких именно «полезных» действий от него «потребуют» на этот раз.
Простейший пример такого рода «неожиданности» - выборка значения из памяти.
При выполнении программы на языке команд процессора необходимость выбрать из памяти значение конкретной переменной выясняется, вообще говоря, не раньше, чем адрес этой переменной встретится в некоторой команде. Уже в следующей команде, скорее всего, будет записана арифметическая операция с выбранным значением. В рассмотренных в первой части настоящего Руководства примерах мы имели дело с памятью, способной выдать значение спустя такт после «предъявления» устройству памяти соответствующего адреса. В универсальных компьютерах, между тем, совершенно нормальной является задержка выдачи значения на 100 и более тактов. В реальных программах простои арифметического устройства на задержках такого рода как раз и занимают основное время работы процессора. Хорошо известные «маленькие хитрости» в реализации современных процессоров (кэш-память, пред-выборка, спекулятивное выполнение команд и т. п.) позволяют во многих случаях эти простои значительно сократить. Но, к сожалению, не устранить совсем.
Между тем, в упоминавшихся примерах из первой части Руководства построенные нами схемы, как правило, не простаивают в ожидании выбираемых из памяти значений ни одного такта. За счет конвейерной организации схемы, необходимые значения просто оказываются на входе соответствующего арифметического устройства именно тогда, когда это устройство способно их принять. Достигается это отказом от самого понятия программы, так или иначе интерпретируемой процессором. Записанные на Автокоде HDL схемы процессорами не являются, и никаких программ не выполняют. Информация о том, какие именно действия, с какими значениями и в каком порядке выполнять, не закодирована в программе, которой нет, а просто учтена (точнее, выражена) непосредственно в структуре заранее построенной схемы.
Процессору, чтобы обеспечить сложение двух чисел, надо:
— выбрать и раскодировать очередную команду,
— «сообразить», чему равны адреса слагаемых,
— доставить слагаемые в сумматор,
— запустить сумматор,
...
В то же время, схеме, в которой две разных памяти заранее присоединены своими выходами к входам сумматора, а регистрами адреса – к соответствующим счетчикам, всю эту «бесполезную» подготовительную работу делать не надо. На очередном такте необходимое сложение запустится само. Это и есть упомянутая нами выше гипотетическая «компиляция программы еще раз», или, выражаясь более правильно, прямая схемная реализация вычислительной процедуры. Нет ничего удивительного в том, что, двигаясь этим путем, можно ускориться в десятки и сотни раз, так что, даже с поправкой на гораздо меньшие, чем у универсальных процессоров, тактовые частоты, ускорение все еще получается многократным.
Таким образом, ускорение расчета при схемной реализации вычислительной процедуры по сравнению с ее программной реализацией получается за счет отказа от интерпретации программы (как и от самой программы вообще). Структура вычислительной процедуры непосредственно отображается в структуру схемы. Если это отображение выполнено удачно, схема будет иметь стопроцентный к.п.д., то есть на каждом такте выполнять «полезные» вычисления.
Как строить эффективные схемы.
Чтобы научиться строить эффективные схемы, принципиально важно изменить привычный для программиста, алгоритмический подход к заданию вычислительной процедуры.
Программа на традиционном языке программирования есть алгоритм, то есть набор последовательно выполняемых шагов. Следующий шаг не начинается, пока не выполнен предыдущий. Это дает невероятную простоту и гибкость в проектировании и записи процедуры, но это же является и причиной потерь, происхождение которых было кратко рассмотрено выше. Записывая вычислительную процедуру в виде алгоритма, то есть последовательности сменяющих друг друга шагов, мы уже почти автоматически лишаемся возможности правильно отобразить структуру вычисления в структуру схемы.
Проектируя схему, следует стараться мыслить не шагами выполнения алгоритма, а тактами (моментами дискретного времени), потоками обрабатываемых данных и функциональными устройствами, такими, как блоки памяти, сумматоры и т. п.
Впервые приступающий к разработке схемы программист обычно старается максимально реализовать ее в разделе последовательных действий, чтобы все было, по возможности, «почти как на Фортране». Как мы видели выше, такой подход сильно ограничивает возможности построения действительно эффективных схем.
В хороших схемах почти всегда раздел последовательных действий невелик и достаточно прост. Основная структура потоков данных должна быть построена заранее, в комбинационной части схемы. Выходы функциональных устройств должны быть поданы на все входы, на которых они могут понадобиться. В разделах последовательных действий и действий на каждом такте осуществляется управление движением этих потоков.
Чтобы понять, на чем основано это управление, рассмотрим основные принципы работы типичного функционального устройства, например, сумматора чисел с плавающей точкой, имеющего два входа и один выход. Сумматор работает постоянно: каждый такт он принимает числа, поступающие на вход, и каждый такт выдает на выход результаты суммирования. При этом сам процесс суммирования занимает, в общем случае, несколько тактов (т.н. задержка устройства). Т.е. для двух конкретных чисел их сумма появится на выходе сумматора через несколько тактов. Поэтому в каждом функциональном устройстве, кроме входов и выхода данных, имеются еще два управляющих сигнала: входной сигнал разрешения и выходной сигнал готовности. Принимая на вход «правильные» данные (сопровождаемые активным сигналом разрешения), сумматор, спустя задержку, активирует выходной сигнал готовности, который будет сопровождать «правильные» результаты. Далее сигнал готовности одного устройства предполагается непосредственно подавать в качестве сигнала разрешения на следующее, потребляющее результаты его работы.
Второй важный аспект построения эффективных схем вычислительного характера – необходимость строить схемы векторно-конвейерного типа.
При построении схем вычислительного характера обычно стараются максимально использовать векторную обработку: пропускать некое поле величин не через одно, а через 2, 4 или 8 идентичных функциональных устройств, работающих одновременно. Каждое такое устройство расходует весомую часть вычислительных ресурсов модуля программируемой логики. Использование устройств с минимальной задержкой приводит к значительному росту таких расходов. Опыт прикладной схемотехники показывает, что разумный компромисс достигается использованием конвейерных устройств с задержкой выдачи результата на несколько тактов. В частности, именно таковы библиотечные устройства плавающей арифметики. Чтобы исключить потери на ожидание каждого отдельного срабатывания такого устройства, циркуляция потоков данных должна быть устроена по конвейерному принципу.
Построение схем.
Построение любой вычислительной схемы делится на две независимые (в смысловом плане) задачи: описание входного интерфейса, т.е. приема данных в схему извне и выдачи результатов из схемы наружу, и обработки данных, т.е. собственно самих вычислений. Описание входного интерфейса – процедура стандартная, почти не зависящая от характера дальнейших вычислений, поэтому рассмотрим ее, не опираясь на конкретные примеры.
Входной интерфейс.
Данные в схему могут поступать либо в виде массивов (в дальнейшем, именно их мы будем называть данными), либо в виде отдельных чисел (в дальнейшем – параметры).
Прием параметров происходит через входные шины регистров A и B (REG_IN_A, REG_WE_A, REG_IN_B, REG_WE_B), а выдача – через выходные (REG_OUT_A, REG_OUT_B). Форма записи приема зависит от того, два или более параметров необходимо принять. Если для вычислений параметры не нужны, то один все равно понадобится: схеме необходимо «сообщить», когда можно приступать к работе. Прием одного или двух параметров записывается в тактированной части схемы.
... [] // раздел действий на каждом такте if(REG_WE_A == 1) my_param1 = REG_IN_A endif if(REG_WE_B == 1) my_param2 = REG_IN_B endif ...
Если в схему надо передать более двух параметров, то один регистр (например B) используется в качестве адреса, а другой (A) – данных. Прием адресов записывается в комбинационной части, а данных – в разделе действий на каждом такте.
... reg_addr = REG_IN_B reg_data = REG_IN_A my_args(1:0) = (REG_WE_B == 1) ? reg_addr(1:0) : my_args(1:0) ... [ ... [] if(REG_WE_A == 1) do @1=0,3 if(my_args == @1) my_param[@1] = reg_data endif enddo endif ...
Выдать из схемы можно не более 2-х параметров. Запись должна быть оформлена в комбинационной части схемы.
REG_OUT_A = result REG_OUT_B = 0
Прием данных происходит через входные шины памяти (DI, ADDR, WE, EN), а выдача – через выходную шину DOUT, при участии входных шин ADDR и EN. Различия в записи приема и выдачи данных зависят от двух условий: один или больше массивов надо принять/выдать, и какова ширина батареи (число блоков) приемных/выходных блоков памяти - единица или больше. Запись этой процедуры происходит в комбинационной части схемы.
Примеры различных вариантов передачи массивов:
// прием: arr.dina[0] = DI arr.addra[0] = ADDR arr.wea[0] = WE // выдача: arr.addra[0] = ADDR DO = arr.douta[0]
// прием: mem_addr = ADDR do @1 = 0, 3 arr.dina[@1] = DI arr.addra[@1](29:0) = mem_addr(31:2) arr.addra[@1](31:30) = 0 arr.wea[@1] = (@1 == mem_addr(1:0) ) ? WE : 0 enddo
Старшие 30 разрядов входных адресов соединены с адресами памяти arr, а младшие 2 разряда обеспечивают последовательную запись 4-х чисел по одному адресу памяти, но в разные блоки этой памяти.
// выдача: mem_addr = ADDR do @1 = 0, 3 arr.addra[@1](29:0) = mem_addr(31:2) arr.addra[@1](31:30) = 0 DO = (mem_addr_out == @1) ? arr.douta[@1] : 'Z' enddo
Здесь появляется еще одна переменная mem_addr_out, в которую записываются 2 младших разряда входного адреса, задержанные на 1 такт. Она отвечает за выбор блока памяти arr, подключаемый к выходу DO. Задержка нужна, т.к. после подачи адреса информация на выходе памяти появится только на следующем такте.
Строка mem_addr_out(1:0) = mem_addr(1:0) должна присутствовать в разделе действий на каждом такте.
// прием: reg_addr = REG_IN_B arr1.dina[0] = DI arr2.dina[0] = DI arr3.dina[0] = DI arr1.addra[0] = ADDR arr2.addra[0] = ADDR arr3.addra[0] = ADDR arr1.wea[0] = (reg_addr == 0 ) ? WE : 0 arr2.wea[0] = (reg_addr == 1 ) ? WE : 0 arr3.wea[0] = (reg_addr == 2 ) ? WE : 0
Как видно из примера 3, распределение входных данных между различными блоками памяти происходит за счет разных значений, подаваемых на регистр 'B'.
// выдача: reg_addr = REG_IN_B arr1.addra[0] = ADDR arr2.addra[0] = ADDR arr3.addra[0] = ADDR DO = (reg_addr == 0) ? arr1.douta[0] : (reg_addr == 1) ? arr2.douta[0] : arr3.douta[0]
Как быть, если память arr необходимо использовать не только для приема входных данных, но и для записи результатов вычислений в ходе работы? Если в комбинационной части переменной присвоено значение, то больше нигде нельзя написать для нее еще одно присваивание. В этом случае используют мультиплексирование, т.е. присваивания объединяются через условие: если условие верно, то выполняется одно присваивание, иначе – другое. Проиллюстрируем это на 1-м примере:
arr.dina[0] = (WE == 1) ? DI : new_data arr.addra[0] = (EN == 1) ? ADDR : new_addr arr.wea[0] = (WE == 1) ? 1 : new_we // или, что то же самое, arr.wea[0] = WE || new_we
Итак, основные принципы построения входного интерфейса изложены. В дальнейшем, из третьей части Руководства можно будет узнать, как избавится от необходимости самостоятельно описывать эту часть схемы, переложив это «бремя» на транслятор.
Вычислительная часть.
Именно к вычислительной части схемы применяется в данном документе понятие эффективность. Ясно, что эффективная схема – это быстро работающая схема. На скорость работы влияют следующие факторы:
- ширина векторной памяти, где будут располагаться данные. Чем шире батарея, тем большее число элементов массива будут вычисляться одновременно;
- количество арифметических операций над массивами, объединенных в один конвейер. Чем конвейер длиннее, тем большее число операций будет выполняться за 1 такт.
Конечно, увеличить ширину батареи просто и скорость возрастет в разы, но в такие же «разы» возрастет и количество вычислительных компонентов, каждый из которых является весьма дорогостоящим удовольствием. Поэтому для сложных схем зачастую приходится рассчитывать, что выгоднее: пожертвовать длинным конвейером (разделив его на две части) ради большей ширины памяти или наоборот.
Так что же такое конвейер? Конвейер – это прохождение одного или нескольких массивов данных (далее - потоков) через ряд последовательно соединенных между собой функциональных устройств (блоков памяти и вычислителей), позволяющих получить ритм выдачи результатов в конце конвейера – один результат за такт. Ритм выдачи не зависит от времени прохождения отдельного числа через конвейер. Под термином – вычислитель далее будем подразумевать библиотечный компонент, выполняющий одну арифметическую операцию над двумя (или одним, в случае извлечения квадратного корня) операндами. В начале конвейера всегда идет считывание данных, в конце – запись результата, в промежутке – вычисления и, в случае необходимости, дополнительные считывания данных и промежуточные записи результатов.
Организация конвейера.
Для организации конвейера, с одной стороны, необходимо соединить потоки данных создаваемого конвейера, подавая выход данных предыдущего устройства на вход последующего. Записывается это в комбинационной части схемы. С другой стороны, продвижением этих потоков нужно управлять. Управление конвейером происходит в тактированной части схемы, но для того, чтобы это стало возможным, в комбинационной части схемы соединяются в цепочку управляющие сигналы – готовность результата предыдущего устройства является разрешением для последующего. При необходимости записи результата в память, сигнал готовности данного результата соединяется с разрешением записи в память.
Управление конвейером можно разделить на два этапа: организация начального запуска и управление движением данных по конвейеру. Такое деление обосновано тем что, запуская конвейер, схема «создает событие», а, управляя движением, схема «реагирует на возникающие события». И в том и другом случае задача управления – обеспечить непрерывную подачу данных, и синхронизировать эти потоки данных и соответствующие им управляющие сигналы (наличие данных соответствует 1 на управляющем регистре, а отсутствие данных соответствует 0 на управляющем регистре). Это ключевая задача построения даже не эффективно работающей схемы, а правильно работающей схемы. Поэтому разберемся в этом вопросе детально.
Непрерывные потоки данных организуются в виде цикла последовательного присваивания адресам памяти значений в нужном диапазоне (далее будем использовать термин – перебор адресов). При считывании управляющий сигнал подстраивается под ритм поступающих выходных данных. При записи – наоборот, поступление данных в память подстраивается под поступивший сигнал готовности. Поскольку запись результатов относится ко 2-му этапу управления, разберем ее ниже, а здесь остановимся на чтении данных.
Допустим, надо сосчитать из блока памяти 100 чисел, лежащих по адресам с 0-го по 99-й. В разделе последовательных действий запись будет следующая:
{
my_addr = 0
}
loopN:
{
if(my_addr < 100)
my_addr++
next loopN
endif
}
Где my_addr – счетчик адресов. Для каждого массива в схеме, данные которого понадобятся для вычислений, заводится свой счетчик адресов считывания (в разделе деклараций объявляется переменная: reg 32 my_addr). В комбинационной части схемы выполняется присваивание, типа:
x.addrb = my_addr
Если для вычислений используются данные нескольких массивов, которые будут подаваться на вычисления одновременно, то один счетчик можно использовать для всех этих массивов. В комбинационной части запись будет типа:
{x.addrb, y.addrb, z.addrb} = my_addr
Теперь встает задача сопроводить поступающие на выход данные единицей на управляющем сигнале. Для этого надо понять, когда на выход поступит первое число и когда – последнее. Если в тактированной части написать a = 5, то на выходе переменной 'a' 5 появится на следующем такте. А если 'a' – это регистр адреса блока памяти, то соответствующее число из памяти появится еще на такт позже. Т.е. при подаче на регистр адреса некоего значения, результат на выходе появится через такт. Начальный адрес у нас подан заранее, поэтому, поставив сигнал разрешения в единицу внутри оператора if, начальную синхронизацию мы отработали (и первое число и разрешение появятся одновременно на 2-м проходе состояния loopN). Когда же надо снимать разрешение? Опять же в силу того, что результат присваиваний отложен на такт, в конце цикла образуется лишняя итерация: то, что my_addr стал = 100, схема «обнаружит» только выполнив еще одну итерацию. Если у оператора if не будет ветки else, то последний такт будет пустым, т.е. не выполняющим никаких присваиваний адресам значений. В нашем случае, на этом такте будет стоять «лишний» адрес 100. В этом случае сигнал разрешения необходимо сбросить в ветке else. Обычно здесь же устанавливается и начальное значение счетчика. Общая запись будет следующей:
{
my_addr = 0
my_we = 0
}
loopN:
{
if(my_addr < 100)
my_addr++
my_we = 1
next loopN
else
my_we = 0
my_addr = 0
endif
}
Если в условии в качестве предельного значения будет указан последний значимый адрес, то сбрасывать управляющий сигнал необходимо в следующем такте:
{
my_addr = 0
}
loopN:
{
if(my_addr < 99)
my_addr++
my_we = 1
next loopN
else
my_addr = 0
endif
}
{
my_we = 0
}
Этот вариант можно использовать для организации итерационного цикла, если нет причин сбрасывать управляющий сигнал после каждого цикла чтения:
{
my_addr = 0
niters = 200
}
loopN:
{
if(my_addr < 99)
my_addr++
my_we = 1
next loopN
else
my_addr = 0
niters--
if(niters > 1)
next loopN
endif
endif
}
{
my_we = 0
}
Здесь niters – число итераций, которое уменьшается на 1 после каждого цикла считывания. Поскольку результат этого вычитания мы узнаем только после еще одного цикла считывания, то условием выхода будет служить niters = 1, а не 0, как в обычной программе.
В случае, когда необходимо использовать ветку else для установления еще одного значимого адреса, то в 0 управляющий сигнал ставится через такт после цикла считывания:
{
my_addr = 1
}
loopN:
{
if(my_addr < 99)
my_addr++
my_we = 1
next loopN
else
my_addr = 0
endif
}
{
}
{
my_we = 0
my_addr = 1
}
Начальный запуск конвейера.
Записывается в разделе последовательных действий. Для этого организуется цикл считывания исходных данных путем перебора адресов на блоках памяти (начальные адреса считывания должны быть поданы заранее), и на этот период устанавливается в единицу исходный сигнал разрешения. По исчерпании адресов сигнал разрешения сбрасывается в 0. Примеры вариантов записи начального запуска были приведены выше.
Управление движением данных.
В простейшем случае управление сводится к записи результатов вычислений в память или регистр (при скалярном результате). В общем случае – это и промежуточные записи результатов, и организация чтения данных для дополнительных вычислений, и перенаправление потоков данных, в зависимости от созревших условий. Все потоки необходимо синхронизировать, чтобы не было простоев и потерь данных. Чем больше действий будет включено в конвейер, тем выше эффективность построенной схемы.
В зависимости от характера действий управление ими описывается в разных частях схемы. В одних случаях можно ограничиться записью соединений в комбинационной части, в других – не обойтись без организации процессов или однократных действий в тактированной части (как правило, пишется это в разделе действий на каждом такте).
В основе выбора действий всегда лежит «реагирование» на возникновение тех или иных управляющих сигналов. Ниже рассмотрим несколько типичных примеров действий по управлению конвейером (в качестве управляющего сигнала возьмем сигнал готовности my_ready, сопровождающий некий результат вычислений my_result).
Запись потока данных в память.
Пишется в разделе действий на каждом такте. Например:
if(my_ready == 1) my_addr_write++ else my_addr_write = 0 // установка начального адреса endif
Где my_addr_write – счетчик адресов записи, в комбинационной части соединенный с адресом памяти;
В комбинационной части сигнал готовности соединен с разрешением записи в память, поэтому, как только он станет =1, откроется запись в память. Настроив начальный адрес заранее (через ветку else), мы обеспечим запись 1-го результата по 0-му адресу на 1-м такте цикла. Одновременно по наличию готовности осуществляется перебор адресов, что обеспечит на следующем такте запись 2-го результата по 1-му адресу и т.д. В память запишется столько чисел, сколько тактов my_ready будет =1. После этого до следующего сигнала готовности на счетчик адресов будет подаваться начальный адрес.
Запись скалярных результатов.
При однократной записи в память вполне достаточно присваиваний в комбинационной части схемы: результат вычислений должен быть соединен с входом данных, на регистр адреса памяти заведен нужный адрес, а сигнал готовности подан на регистр разрешения записи в память.
Запись результата в регистр (reg_save) можно оформить как в тактированной части схемы (в зависимости от ситуации, это может быть и разделом действий на каждом такте, и разделом последовательных присваиваний):
if(my_ready == 1) reg_save = my_result endif
так и в комбинационной части:
reg_save = (my_ready == 1) ? my_result : reg_save
Считывание данных из массива.
Пишется в разделе действий на каждом такте. Применяется, когда в очередном вычислении участвуют данные из памяти и результаты другого вычисления. Цикл перебора адресов записывается так же, как и в случае записи в память:
if(my_ready == 1)
my_addr_read++
else
my_addr_read = 0
endif
Где my_addr_read – счетчик адресов считывания,
my_ready – сигнал готовности предыдущего вычисления.
Но здесь возникает проблема с синхронизацией дальнейшего вычисления: считанные числа из памяти пойдут с задержкой на 1 такт относительно результатов предыдущего вычисления. Выдавать их раньше не получится, поэтому остается задержать на такт результаты и сопровождающую их готовность. Общая запись будет такой:
my_result_delay = my_result
my_ready_delay = my_ready
if(my_ready == 1)
my_addr_read++
else
my_addr_read = 0
endif
А в комбинационной части my_result_delay и my_ready_delay подать на следующий вычислитель в качестве входных данных и сигнала разрешения.
В схеме может быть задействован не один конвейер, а больше (типичный случай – необходимо просуммировать все элементы одного массива, а потом для каждого элемента другого массива выполнить арифметическую операцию с участием полученной суммы). В таких случаях, в целях экономии, надо стараться использовать одни и те же вычислители в разных конвейерах. Эта экономия позволит увеличить векторную обработку данных. Тогда в комбинационной части на входы таких вычислителей различные данные должны подаваться через условие (мультиплексирование). В тактированной части, управляя этим условием, можно добиться подачи на вычислитель то одних данных, то других.
Теперь попробуем проиллюстрировать систематическое применение этих общих принципов на конкретных примерах. Обратимся опять к задаче вычисления интеграла.
Итак, имеется массив действительных чисел. Необходимо 1-й и последний элементы массива разделить на два, затем весь массив суммировать, а потом полученный результат разделить на размер массива. Запишем эту задачу в виде цепочки действий:
начальные действия (умножение на 0.5 двух чисел, ожидание результата и запись в память)
основные действия (суммирование массива)
завершающие действия (деление полученной суммы на число элементов, ожидание результата и запись его на выходной регистр).
Из приведенной цепочки видно, что конвейер можно сделать из процесса суммирования. Время всей работы будет складываться из времени работы каждого из трех действий. Можно ли здесь сэкономить? Можно, если включить в конвейер начальные действия, т.е. выполнять их на фоне суммирования (включить в конвейер деление не удастся, т.к. пока суммирование не закончится, к делению приступать нельзя). Экономия, правда, здесь небольшая, но для демонстрации повышения эффективности схем, имеет смысл рассмотреть именно этот вариант.
Что нам понадобится от внешней программы:
- массив данных – примем его в ram arr (ширина батареи 8);
- размер массива – примем его в регистр count;
- адрес последнего числа в массиве – примем его в регистр last_addr. Для удобства передадим его как N/8 - 1, где N – размер массива (воспользоваться значением count не удастся, т.к. передаваемый размер массива должен быть в формате действительного числа).
- Результат вычислений сохраним в регистре divide.
Для вычислений нам понадобятся:
- вычислитель floating32_mul – для умножения;
- вычислитель floating32_div – для деления;
- 8 вычислителей floating32_add – для организации сложения массива.
Начнем строительство нашего конвейера с суммирования. Из общих соображений структурного проектирования выделим эту часть схемы в отдельный компонент. Такой подход позволяет существенно разгрузить описание основной схемы, сделав его более наглядным и читабельным. Имя компонента может быть любым, разумеется, пересечение имен с библиотечными компонентами недопустимо. Назовем его - my_summator.
Заголовок компонента:
program my_summator in 32 DIN0 in 32 DIN1 in 32 DIN2 in 32 DIN3 in 32 DIN4 in 32 DIN5 in 32 DIN6 in 32 DIN7 out 32 DOUT in 1 EN out 1 RDY in 0 Clk in 0 Reset endprogram
С входов DIN0 - DIN7 в компонент будут поступать числа из памяти для суммирования. На выход DOUT мы подадим результат сложения. Управляющие сигналы EN и RDY – это, соответственно, входной сигнал разрешения и выходной сигнал готовности. Сигнал Clk – это источник тактов, он нужен всегда, а сигнал Reset отвечает за начальный сброс, в этой схеме он понадобится.
Начинаем выстраивать конвейер. Для начала сложим 8 входных потоков в один. Поскольку складывать 8 чисел можно несколькими способами, то встает вопрос, какой из них самый предпочтительный? Допустим, надо сложить: a+b+c+d. Можно сначала сложить a+b, через 5 тактов (задержка сумматора) к сумме +c, а еще через 5 тактов к новой сумме +d. А можно параллельно сложить a+b и c+d, а через 5 тактов сложить две одновременно появившиеся суммы. Число сумматоров для обоих вариантов будет одинаковым (3), но 2-й вариант предпочтительней. В общем случае, при формировании арифметического выражения руководствоваться надо следующими соображениями:
- Все, что можно делать параллельно, нужно делать параллельно.
- Желательно, чтобы входные ветви вычислителя были равновесными, т.е. чтобы к одному вычислителю оба операнда подходили бы одновременно, потому что, если один из них поступит раньше другого, его необходимо будет задержать до прихода второго. К примеру, задержка в 5 тактов - это 5 регистров, последовательно соединенных в тактированной части схемы, через которые первый операнд должен будет пройти, прежде, чем попасть на вычислитель. Понятно, что второе условие далеко не всегда выполнимо, но стремиться к этому надо.
Для наглядности изобразим оптимальное суммирование в виде блок-схемы:
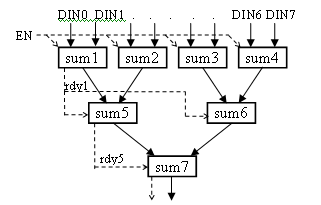
Из этой блок-схемы ясно видно, как должны быть связаны входные и выходные данные сумматоров. Для sum1-sum4 разрешением будет служить внешний сигнал EN. Поскольку задержки всех сумматоров одинаковы, то разрешением для sum5,sum6 будет готовность от sum1, а для sum7 - готовность от sum5. Таким образом, сигнал готовности rdy7 станет равной единице тогда, когда на выходе sum7 появится первый результат и будет активен ровно столько, сколько тактов будет активен входной сигнал EN.
Напишем эту часть схемы:
declare
component floating32_add
reg 32 partsum(15)
reg 1 enable(8)
enddeclare
enable[0]=EN
partsum(0:7)={DIN0,DIN1,DIN2,DIN3,DIN4,DIN5,DIN6,DIN7}
do @1=0,6
insert floating_add
.a(partsum[@1*2])
.b(partsum[@1*2+1])
.operation_nd(enable[(@1/4)+(@1/6)*4](0))
.rdy(enable[@1+1](0))
.result(partsum[@1+8])
.clk(Clk)
endinsert
enddo
Все входы и выходы данных расположены в одном векторном регистре partsum(15), а разрешения и готовности - в одном векторном регистре enable(8), исключительно ради краткости записи.
Теперь на выходе partsum[14] мы имеем поток частичных сумм, сопровождаемый сигналом готовности enable[7]. Для сложения этого потока в одну сумму понадобится еще один сумматор, на один вход которого будут поступать числа из потока, а на другой - свой же результат суммирования. Поскольку сумматор имеет задержку, то на тот период, когда данные на 1-й вход уже поступают, а результат 1-го суммирования еще не готов, на 2-й вход надо подавать 0. Если бы сумматор имел задержку 1 такт, задачу суммирования можно было бы считать решенной. Но, т.к. она 5 тактов, придется еще решить задачу окончания суммирования, когда поток уже закончился, а с выхода сумматора еще 5 тактов последовательно поступают частичные суммы, которые тоже надо сложить. Для решения этой задачи нам придется написать процесс в тактированной части схемы.
declare
reg 32 L(2)
reg 32 WW
reg 32 last_sum
reg 0 last_rdy
reg 0 enin
reg 1 sum_rdy
reg 5 step
enddeclare
insert floating32_add
.a(L[0])
.b(L[1])
.operation_nd(enin)
.rdy(last_rdy)
.result(last_sum)
.clk(Clk)
endinsert
DOUT=WW
RDY=sum_rdy
// на 1-й вход подаем поток, если он есть, иначе - задержанный на 1 такт выход
// (для последних пяти суммирований):
L[0]= (enable[7]==1) ? partsum[14] : WW
// на 2-й вход подаем 0, если поток есть, а результата еще нет, иначе – выход сумматора:
L[1]= (enable[7]==1 && last_rdy==0) ? 0 : last_sum
// разрешение на входе сумматора равно единице либо когда есть поток, либо когда
// совпадает готовность сумматора и нечетное значение счетчика тактов
// (для последних 5-ти суммирований), иначе - 0:
enin = (enable[7]==1 || (step(0)==1 && last_rdy==1)) ? 1 : 0
[
step=0 // начальное обнуление счетчика (для этого нужен сигнал Reset)
[]
if(enable[7]==1) // выясняем удвоенную величину задержки сумматора:
if(last_rdy==0) // пока поток есть, а суммы еще нет,
step+=2 // каждый такт прибавляем к счетчику 2
endif
else
if(last_rdy==1) // окончание суммирования, когда потока нет, а суммы идут:
WW = last_sum // для правильной подачи данных задерживаем на такт выход,
if(step>2) // а для генерации сигналов разрешения, на каждом такте уменьшаем
step-- // значение счетчика на 1, пока он не станет равным 2
else
step=0 // сбрасываем счетчик в 0, чтобы выходная готовность длилась 1 такт
endif
endif
endif
// формируем однотактную готовность, которая будет сопровождать
// окончательную сумму:
if(enable[7]==0 && last_rdy==1 && step==2)
sum_rdy=1
else
sum_rdy=0
endif
В готовом виде компонент my_summator будет выглядеть так:
in 32 DIN0
in 32 DIN1
in 32 DIN2
in 32 DIN3
in 32 DIN4
in 32 DIN5
in 32 DIN6
in 32 DIN7
out 32 DOUT
in 1 EN
out 1 RDY
in 0 Clk
in 0 Reset
endprogram
declare
component floating32_add
reg 32 partsum(15)
reg 32 L(2)
reg 32 WW
reg 32 last_sum
reg 1 enable(8)
reg 0 last_rdy
reg 0 enin
reg 1 sum_rdy
reg 5 step
enddeclare
enable[0]=EN
DOUT=WW
RDY=sum_rdy
partsum(0:7)={DIN0,DIN1,DIN2,DIN3,DIN4,DIN5,DIN6,DIN7}
do @1=0,6
insert floating32_add
.a(partsum[@1*2])
.b(partsum[@1*2+1])
.operation_nd(enable[(@1/4)+(@1/6)*4](0))
.rdy(enable[@1+1](0))
.result(partsum[@1+8])
.clk(Clk)
endinsert
enddo
insert floating_add
.a(L[0])
.b(L[1])
.operation_nd(enin)
.rdy(last_rdy)
.result(last_sum)
.clk(Clk)
endinsert
L[0]= (enable[7]==1) ? partsum[14] : WW
L[1]= (enable[7]==1 && last_rdy==0) ? 0 : last_sum
enin = (enable[7]==1 || (step(0)==1 && last_rdy==1)) ? 1 : 0
[
step=0
[]
if(enable[7]==1)
if(last_rdy==0)
step+=2
endif
else
if(last_rdy==1)
WW = last_sum
if(step>2)
step--
else
step=0
endif
endif
endif
if(enable[7]==0 && last_rdy==1 && step==2)
sum_rdy=1
else
sum_rdy=0
endif
Далее этот текст следует сохранить в файле под именем my_summator.avt и выполнить команду make_headfile my_summator.avt, которая создаст заголовочный файл для этого компонента и поместит его в директорию заголовочных файлов USERCOMPONENTS. Ознакомившись с третьей частью Руководства, можно будет узнать, что вычислительные компоненты транслятор то же умеет создавать сам.
Вернемся теперь к описанию конвейера в основной схеме. В комбинационной части надо связать память arr во-первых с компонентом my_summator (для суммирования), а во-вторых - с компонентом floating32_mul (для умножения и записи результатов в память). Для выполнения этой задачи используем в памяти arr оба порта: для умножения – порт “a”, для сложения – порт “b”.
1. Суммирование.
do @1=0,7 my_sum_in[@1]=arr.doutb[@1] arr.addrb[@1]=addr_read enddo
Для вычисления суммы все выходы памяти подаем на входы нашего компонента, а на адресную шину – регистр addr_read, который будет служить счетчиком адресов.
2. Умножение.
// если адрес считывания addr_read равен 2, // подаем на вход умножителя последнее число, иначе – первое: mul_in= (addr_read==2) ? arr.douta[7] : arr.douta[0] arr.dina[0]=mul_out // для записи результатов умножения arr.dina[7]=mul_out // подаем выход умножителя на входы памяти arr.addra[0]=0 // записываем первый и последний адрес на шину адреса arr.addra[7]=last_addr // памяти для считывания и последующей записи. // формируем разрешение записи в память для 1-го результата: arr.wea[0] = (addr_read == 8) ? 1 : 0 // формируем разрешение записи в память для 2-го результата: arr.wea[7] = (addr_read == 7) ? 1 : 0Регистр addr_read будем использовать как счетчик тактов, поэтому управляющие сигналы для умножителя не понадобятся. Заменив на входе умножителя последнее число на первое при addr_read = 2 и подав на вход разрешения записи в память единицу при соответствующих значениях addr_read (зная, что задержка умножения 5 тактов), запись в память нужных результатов мы обеспечим без управляющих сигналов.
insert floating32_mul
.a(mul_in)
.b(float(0.5))
.result(mul_out)
.operation_nd('1')
.rdy(open)
.clk( Clk )
endinsert
Для того чтобы в суммировании участвовало новое значение 1-го числа, достаточно будет изменить порядок считывания: цикл чтения данных начнется с адреса addr_read=1, а закончится адресом addr_read=0.
Следует отметить, что все присваивания в память arr по порту “a” в окончательной записи будут дополнены приемом внешних данных.
В комбинационной части осталось подать результат суммирования на вход делителя, а готовность суммы на разрешение деления.
insert floating32_div .a(my_sum_out) // подаем на 1-й вход делителя выход нашего сумматора .b(count) // на 2-й вход подаем число элементов массива .operation_nd(my_sum_rdy(0)) // готовность суммы подаем на разрешение деления .rdy(div_rdy(0)) // готовность результата деления .result(div_out) // результат деления .clk(Clk) endinsert
Все соединения в комбинационной части, необходимые для непрерывной работы схемы сделаны, осталось написать процесс, который будет управлять работой конвейера.
[ // раздел начального сброса
addr_read = 1 // устанавливаем начальный адрес чтения
my_sum_we = 0 // сбрасываем сигнал разрешения записи в сумматор
[] // раздел действий на каждом такте
if(div_rdy == 1)
divide = div_out // записываем результат деления на выходной регистр
endif
] // раздел состояний
loop0:
{
my_sum_we = 1 // ставим сигнал разрешения записи в сумматор
if(addr_read<last_addr) // организуем цикл по перебору адресов массива,
addr_read++ // подавая на каждом такте на вход сумматора по 8 чисел
next loop0
else
addr_read = 0 // в конце цикла считываем первые 8 чисел
endif
}
{ // по выходу из цикла ставим пустой такт для синхронизации
}
loop1:
{
my_sum_we = 0 // снимаем разрешение записи
}
Вычислительная часть схемы написана. В окончательном виде, с учетом входного интерфейса и соединения схемы с компонентом my_summator, описание схемы будет выглядеть так:
program vector_proc_32
out 32 DO
in 32 ADDR
in 32 DI
in 1 EN
in 1 WE
in 32 REG_IN_A
out 32 REG_OUT_A
in 1 REG_WE_A
in 32 REG_IN_B
out 32 REG_OUT_B
in 1 REG_WE_B
in 0 Clk
in 0 Reset
endprogram
declare
component floating32_mul
component floating32_div
component my_summator
ram 32 arr(8,16384)
reg 32 mul_in
reg 32 mul_out
reg 32 my_sum_in(8)
reg 32 my_sum_out
reg 1 my_sum_we
reg 1 my_sum_rdy
reg 32 div_out
reg 1 div_rdy
reg 32 ready
reg 32 divide
reg 32 count
reg 32 last_addr
reg 32 addr_read
reg 32 reg_addr
reg 32 reg_data
reg 1 reg_args
enddeclare
reg_addr = REG_IN_B
reg_data = REG_IN_A
reg_args(0) = (REG_WE_B == 1) ? reg_addr(0) : reg_args(0)
REG_OUT_B = ready
REG_OUT_A = divide
arr.dina[0] = (WE==1) ? DI : mul_out
arr.dina[7] = (WE==1) ? DI : mul_out
arr.addra[0](28:0) = (EN==1) ? ADDR(31:3) : 0
arr.addra[7](28:0) = (EN==1) ? ADDR(31:3) : last_addr(28:0)
arr.wea[0] = (ADDR(2:0)==0 && WE == 1) ? 1 : (addr_read == 8) ? 1 : 0
arr.wea[7] = (ADDR(2:0)==7 && WE == 1) ? 1 : (addr_read == 7) ? 1 : 0
do @1=1,6
arr.dina[@1] = DI
arr.addra[@1](28:0) = ADDR(31:3)
arr.wea[@1] = (@1 == ADDR(2:0) && WE == 1) ? 1 : 0
enddo
mul_in= (addr_read == 2) ? arr.douta[7] : arr.douta[0]
insert floating32_mul
.a(mul_in)
.b(float(0.5))
.result(mul_out)
.operation_nd(‘1’)
.rdy(open)
.clk( Clk )
endinsert
insert floating32_div
.a(my_sum_out)
.b(count)
.operation_nd(my_sum_rdy(0))
.rdy(div_rdy(0))
.result(div_out)
.clk(Clk)
endinsert
insert my_summator
.DIN0(my_sum_in[0])
.DIN1(my_sum_in[1])
.DIN2(my_sum_in[2])
.DIN3(my_sum_in[3])
.DIN4(my_sum_in[4])
.DIN5(my_sum_in[5])
.DIN6(my_sum_in[6])
.DIN7(my_sum_in[7])
.DOUT(my_sum_out)
.EN(my_sum_we)
.RDY(my_sum_rdy)
.clk( Clk )
.Reset(Reset)
endinsert
do @1=0,7
my_sum_in[@1]=arr.doutb[@1]
arr.addrb[@1]=addr_read
enddo
[
last_addr = 0
my_sum_we = 0
[]
if(REG_WE_A == 1)
if(reg_args == 0)
count = reg_data
else
last_addr = reg_data
ready = 0 // сбрасываем код завершения работы в 0
endif
endif
if(div_rdy==1)
divide = div_out
ready = 1 // возводим код завершения работы в 1
endif
]
loop0:
{
if(last_addr==0) // чтобы начать работу, дожидаемся
next loop0 // приема последнего параметра
addr_read = 1 // устанавливаем начальный адрес чтения здесь, чтобы
endif // сохранить возможность повторного вычисления
}
loop1:
{
my_sum_we=1
if(addr_read<last_addr)
addr_read++
next loop1
else
addr_read=0
endif
}
{
}
loop2:
{
my_sum_we=0
last_addr=0
next loop0 // возврат в начало процесса (в фазу ожидания)
}
Сохраним текст программы в файле под именем my_integral.avt и схема вычисления интеграла готова к трансляции:
avto my_integral.avt my_summator.avt
Внешняя, вызывающая программа будет иметь приблизительно такой вид:
#include <stdio.h>
#include "comm.h"
#define LARR (16384)
#define L (8)
int fpga_main( void )
{
static float arr[LARR];
int result, i, adr, ans=0;
float count;
for (i = 0; i < LARR; i++)arr[i] = i+1;
count=LARR;
adr=(LARR/L) -1;
to_coprocessor( 0, arr, LARR );
to_register(7,0);
to_register(6,*((int *)(&count)));
to_register(7,1);
to_register(6,adr);
while(!ans) from_register(7,&ans);
from_register(6,&result);
printf("result:%f\n",*((float *)(&result)));
return 0;
}
В заключение отметим, что приведенные выше рекомендации, отнюдь не исчерпывают всех способов построения схем. Для построения реальных задач с множеством сложных вычислений зачастую приходится придумывать свои «маленькие хитрости», чтобы добиться желаемого результата. Надеемся, что типовые приемы программирования, изложенные в настоящем документе, послужат для этого хорошим подспорьем.